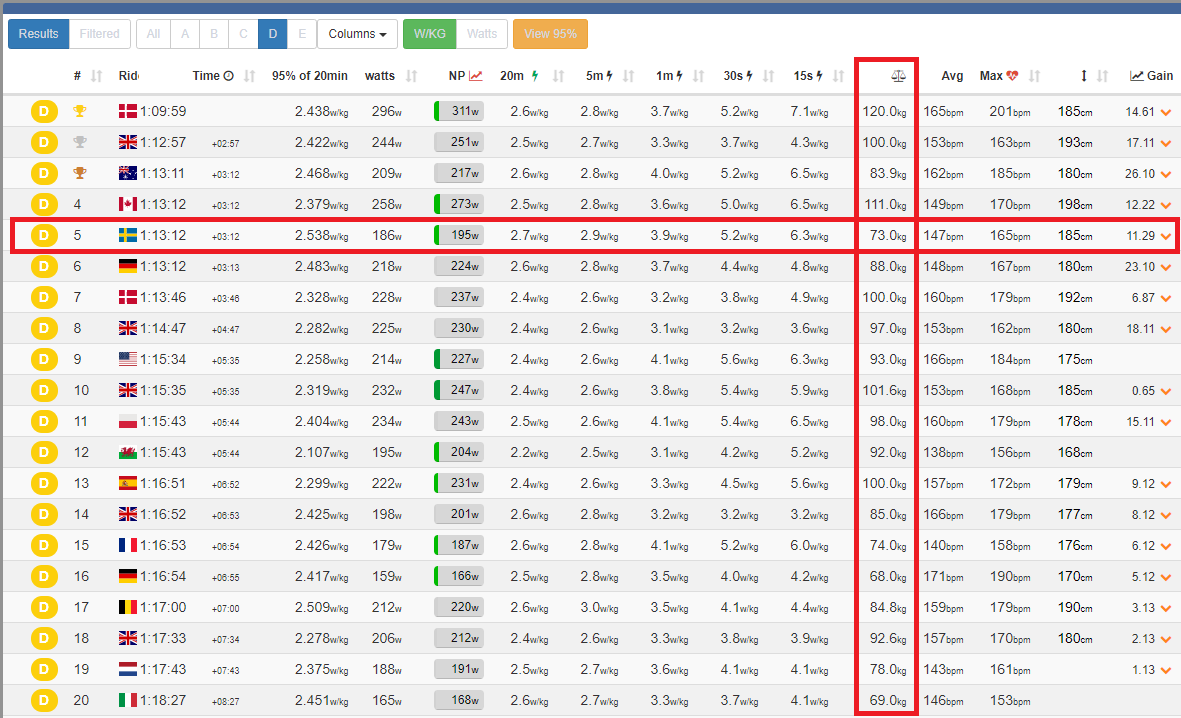
In the previous lesson we learned how to manage the trailing 20 min W/kg average so that the highest such trailing average in a race does not reach the performance ceiling in your cruising cat.
We made the distinction between 20 min blocks on the one hand, which any race can be divided into, and on the other hand 20 min periods, or trailing 20 min averages, which is what ZP measures and which can intersect two 20 min blocks.
We also said that in most races the highest 20 min period in your race, which ZP will judge you by, is likely going to coincide with the first 20 min block since it includes the start, where everyone typically pushes hard for early positioning, thus driving up the average.
But is it optimal to push hard the first 20 min? What does in-game physics have to say? Let’s find out!
Zwift physics is modeled on real life cycling physics. I wouldn’t say this has been tested thouroughly yet, but all the little studies so far, and some of them you can find on Zwift Insider if you dig around, indicate that, although with some convenient simplifications, Zwift closely follows the generally accepted physics model of cycling, parts of which was published in a report by Martin et al (1998) but which is fundamentally plain old Newtonian physics. And this matters because it helps us make a crucial (cruisial) prediction regarding the first 20 min of the standard race.
I’ll throw some physics in your face:

These hieroglyphics are not nearly as difficult as they may seem at first, so bear with me for a minute. The above formula can be used to calculate the power in Watts needed to pedal your virtual Zwift bike forward on a flat surface, a simplified case but the Tick Tock course does spring to mind. Let’s pick the formula apart.
P is power in Watts. Fv or F * v is force, measured in Newton (like on your expensive Park Tools torque wrench), times your speed. They are the same. It’s how you can define Watt.
Then comes an expression in two parts. First is the Cr * m * g * v. It’s the contribution of rolling resistance. Friction between wheels and tarmac and friction within the drive chain means you don’t get fully rewarded with speed when you pedal. Some is lost due to rolling resistance and you need to counter it. Little is known about how rolling resistance is modeled in Zwift and it really doesn’t matter for our purposes. Likely it’s just a fixed number regardless of rider and chosen bike. For simplicity, let’s assume it is zero, no rolling resistance to worry about.
Then comes the second part of the formula on the right hand side, and this is where it gets interesting. The second part says something about air resistance, or drag. There is no wind in Zwift but it seems drag is accurately modeled.
The second part of the expression is ½ * Cd * rho * A * v^3. (It’s not a ‘p’, it’s the Greek letter rho, but that’s unimportant.) What does it all mean?
Cd is the drag coefficient. Every 3D geometrical shape, or its front side rather, has its unique Cd, we could say. A low number is preferable because that means we will need to push a lower P, Watt, to keep the bike moving. A ball-shaped object has a lower Cd than a cubic object, e.g. a cardboard box. A pointy bullet or a rocket has an even lower Cd than a ball. And an aero bike frame has a lower Cd than a MTB. What about the rider? Even though it is a simplification, Zwift most likely sets a fixed number for any rider regardless of their real-life bodily shape.
The funny looking ‘p’, rho, is air density. The thickness of the air. We don’t normally think about air and the resistance it actually gives unless we take a walk on a windy day. Or when we get on the bike outdoor and try to be fast. In complete vacuum, like in outer space, rho would be zero, because there is no air at all there. And when you multiply something by zero, it becomes zero. So if rolling resistance is zero, which we assumed for simplicity, and if there is no air, then no power is needed to keep a certain speed on your space bike. You just need to worry about the initial acceleration up to the speed you want to keep, but that’s a different formula. This is the reason why it is possible to go back to Earth from the Moon without a crap ton of fuel or why a satellite can go around the Earth at very high speeds without using any engines – in vacuum you just keep going. But down here on Earth we have to keep applying Watts to keep the speed. And the closer to sea level we are, the higher the air resistance because the air density is slightly higher due to gravity, whereas the density is slightly lower at high altitude. So what about Zwift? The Zwift physics model is probably simplified, meaning air density is just a fixed number regardless of whether you ride the Ocean tunnel or sprint to the finish on Ven Top.
Next comes the constant A. That is you and your bike’s frontal area measured in square meters. A big frontal area gives high air resistance. This is how a sailing boat can go forward without an engine. A huge frontal (or aft) area in the form of the sails, the bigger the better, sort of. But for a bike rider you want it as small as possible. Aero frame. Aggressive riding posture. Etc. Like with Cd, the drag coefficient, a smaller frontal area means you can push lower Watts to keep a certain speed. Frontal area has been shown to vary among bikes and riders in Zwift. A short rider is more aerodynamic because he has a smaller frontal area. Possibly, although not quite confirmed, a tall light rider has a smaller frontal area than a tall heavy rider in Zwift. Outdoors this is so. But regardless, like with the drag coefficient and air density, this is a constant that you cannot change (unless you lower your height in the Zwift settings). These factors are what they are for you in any race.
So what the hell does all this have to do with the first 20 min when cruising a race? Well, there is one more factor to consider, the cruisial one. Next and finally comes v^3, velocity (or speed in meters per second) raised to the third. A cubic speed. And this has huge implications for Zwift racing in general and for the first 20 min when cruising.
Let’s visualize with the help of some fictitious and simplified (an thus unrealistic but illustrative) examples. Let’s assume rolling resistance is zero. Let’s assume Cd, rho and A are all 1. So then the Watt needed to keep a certain speed, v, is:
P = 0 + ½ * 1 * 1 * 1 * v^3
which is the same as
P = ½ * v^3
So under these artificial circumstances, the Watts needed to keep 25 kph would be:
P = ½ * …
Wait a minute. v is measured in m/s in Newtonian physics, not kph. We need to convert 25 kph to m/s. 25 kph = 6.9 m/s.
P = ½ * 6.9^3 = 164W
These are unrealistically high Watts. That’s just because we set the other factors to 1. They are constant and don’t change and they are lower than 1 in reality. But it keeps the example simple, so let’s stick with those numbers.
What about keeping 30 kph instead? 30 kph = 8.3 m/s.
P = ½ * 8.3^3 = 286W
But that’s no way to start a race. If we were to race a TT without drafting in the lower categories we might want to go at 35 kph. 35 kph = 9.7 m/s.
P = ½ * 9.7^3 = 456W
In a normal race we would be drafting in a group as cruisers. So we would probably be looking at 40 kph on the flat mid-race rather than 35 kph. 40 kph = 11.1 m/s.
P = ½ * 11.1^3 = 683W
But we were supposed to talk about the first 20 min. At the start everybody will be pushing hard. We would want to go at 45 kph at least to keep up with the others. 45 kph = 12.5 m/s.
P = ½ * 12.5^3 = 977W
Nah, let’s stomp it at start and sail with the sandbaggers for a bit and then compensate the high initial Watts by going under cat limit for the latter part of the first 20 min. Let’s do 50 kph at start! 50 kph = 13.9 m/s.
P = ½ * 13.9^3 = 1342W
Hmm… there is something going on with the Watts needed. And it has to do with raising speed to the third in the formula. Let’s visualize it in a graph.

We can see that the line is not straight. The relationship between speed and the Watts needed to keep it is not linear. It’s cubic. This means that for every additional kph we want to add to your speed, the Watts needed to drive it grows exponentially. It is not hard to keep 20 kph even without drafting. To increase speed by 10 kph to a total of 30 kph is harder but still not hard. But to increase with yet another 10 kph up to 40 kph is notably harder even though the speed increase (10 kph) is the same in both cases. And going 50 kph without drafting starts to get really hard. For some people it will mean actually sprinting, something you can’t keep up for long.
So what about the first 20 min then? Let’s simplify again. Assume that the cat limit translates into the W/kg needed to go 40 kph. And assume that you have the choice between going a steady 40 kph throughout the first 20 min and going 50 kph for the first 10 min and then 30 kph for the last 10 minutes to compensate for the hard start. (50 + 30 ) / 2 = 40, so the average speed would be the same in both cases.
In the first case, a straight 40 kph for 20 min, would mean 683W with our simplified and exaggerated numbers. And let’s say 690W is the cat limit. You have nearly optimized the first 20 min then, all else equal.
But what about the hard-start option then? For the first 10 min you go at 50 kph, meaning 1342W, and then 30 kph meaning 286W for another 10 min.
(1342 + 286) / 2 = 814
So by going hard rather than keeping an even pace in the first 20 min, your Watts needed jump from 683W to a whopping 814W! And if the cat limit for you with your weight was 690W, then you would go over limit by a mile and get a WKG on ZP.
In a real Zwift race the drag coefficient and the other constants will be lower, so the actual Watts needed will be lower of course. But the cubic relationship between Watts and speed remains the same. It is much more efficient to keep an even speed just below limit in the first 20 min block of a race, or actually at any point in a flat race.
But…
Can you? There could also be tactical considerations to take into account, things that might force you to go hard at start. Let’s assume, again simplified, that at start you have the choice between two groups. The front group is full of sandbaggers and will keep a speed above your limit, so you can’t stay with it for long. But later in the first 20 min the group will shatter into two and you could go with the slower subgroup and keep within limits. Or you could go with the second group which ends up traveling at a decent margin below cat limit. Although going with group two will safeguard your average, you will be going too slow later in the race and will probably miss the podium. Trying to bridge to the slower part of the front group from group two would mean pushing very hard Watts solo without draft later and might not be possible.
So there are reasons, fuzzy uncertain factors to consider, when choosing speed in the first 20 min block. But you should be aware of the… let’s give it a cool name, the Cubism of Speed, when you cruise. The best thing to do is rarely to go with the worst bunch of the sandbaggers at the start, even if you intend on dropping later in the first 20 min block. It is a better choice to look for a somewhat slower group already from the start, a group that you will have to drop into later anyway as you drop from the sandbaggers. And when you have dropped into that somewhat slower group, your average will be higher than theirs because of your early sins at the start. Very important point! So it would have been better to go with the slower group already from the start. Going too hard at start is a complete waste of useful W/kg wiggle room as a cruiser. It is what is going to prevent you from having to drop to save your average if there is an early climb, or what is going to prevent you from bridging to a somewhat faster group if it turns out your group slows down too much.
But what about drafting? Drafting means you get less air resistance, right? So how does that affect the whole argument? If you can secure good drafting in the first 20 min, wouldn’t it change things? No. Well, a little bit. But in the two group example we assumed draft in both groups. And the way draft is calculated in Zwift, it seems it gives at best something like a 30% reduction in drag. But even so the cubic relationship between Watts and speed remains, although with this reduction. If the choice is between going with a fast group in draft and going solo behind them at start, then provided the fast group doesn’t send you over limit, in which case you would have to drop anyway, then going with the group is the better option because of the 30% reduction. But in most cases when cruising you should avoid taking wind like the plague anyway, regardless of which group you choose to go with. Cruisers suck wheels and only take wind when attacking.
So how do you choose the optimally paced group at start then? Well, that is more an art form than science, at least then and there from the saddle with numbers and riders flashing on the screen all over. It will take a lot of practice. Practice with caution. Err on the side of prudence, push it slightly more in the next race instead and you will have a long and fruitful career as a cruiser. Good luck!